Mil maneres de representar la Terra

La manera més fàcil de representar el nostre planeta és tal com és: amb un globus –una esfera–. Però la cosa es complica quan l’hem de representar en un suport pla –un full o una pantalla– per poder tenir el que coneixem com a mapa. La resposta a “Quin és el plànol del món més correcte?” o “Quin mapamundi és més similar a la realitat?” és confusa: tots o cap. Qualsevol projecció cartogràfica del nostre planeta és una simulació, una eina per a una funció concreta.

Projecció: d’una esfera a un pla

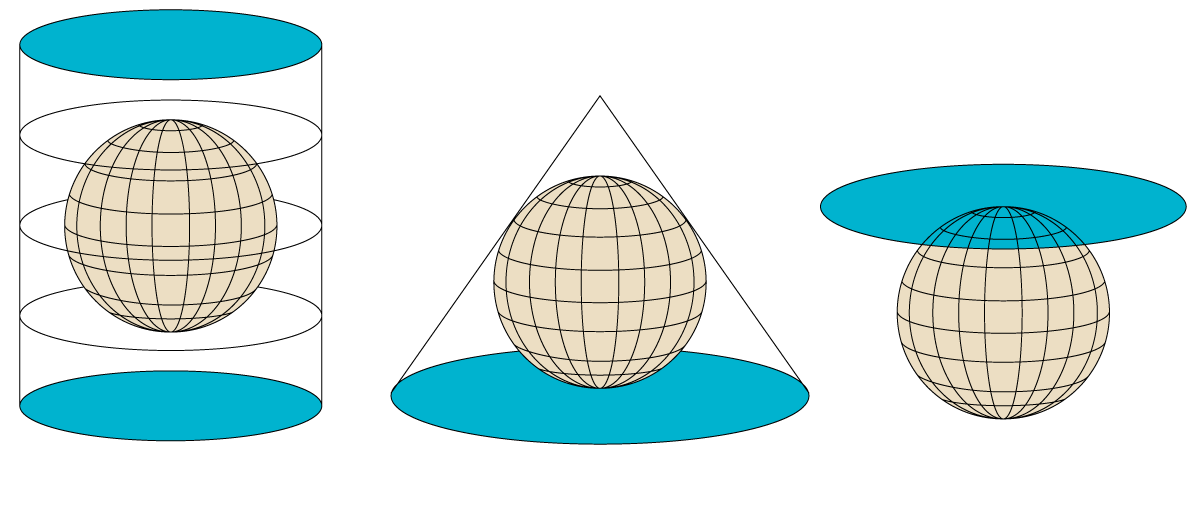
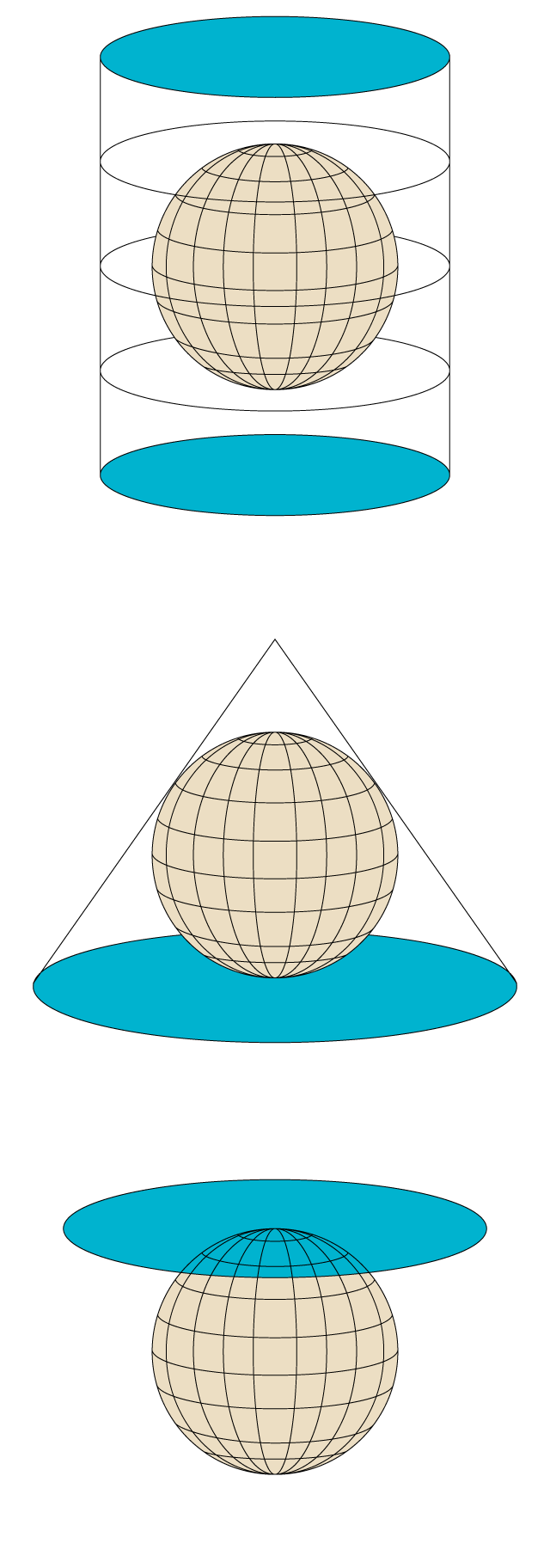
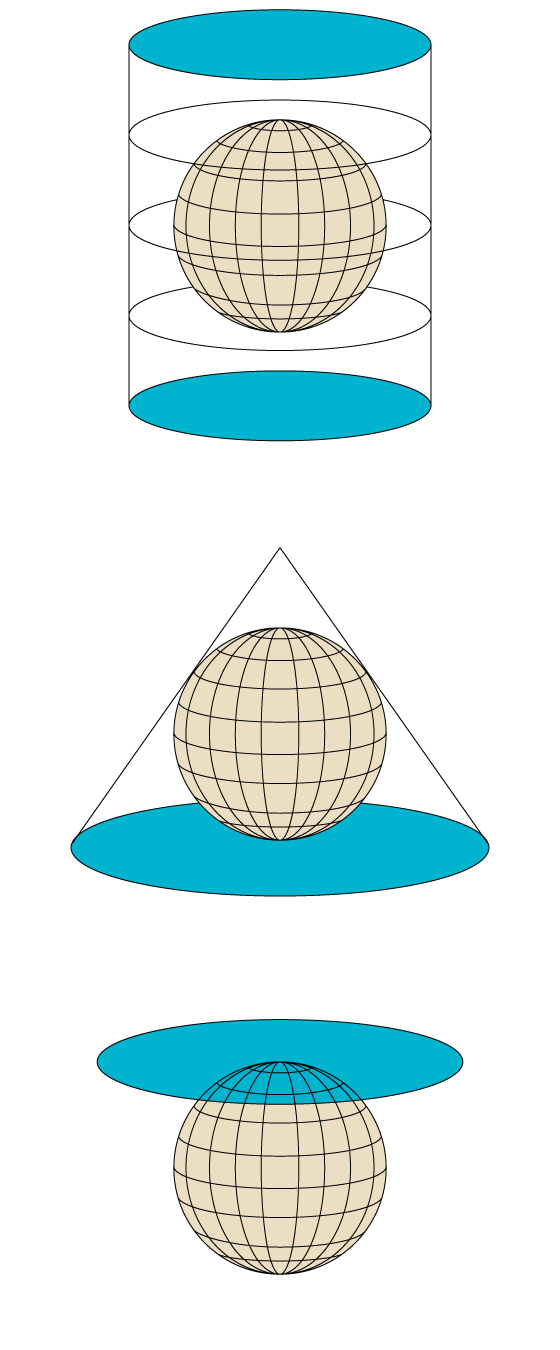
Una projecció és un procediment matemàtic (per tant, exacte) per representar la superfície de la Terra, que és esfèrica, sobre un mapa, que és una superfície plana. Segons el model conceptual, hi ha tres tipus principals de projeccions.

Com que la representació d'una superfície esfèrica sobre una superfície plana mai podrà ser totalment fidel, una projecció sempre deforma o distorsiona com a mínim una de les següents propietats.

• Forma: L’orientació dels angles ens ajuda a reconèixer visiblement països i zones concretes. Per conservar millor la forma, cal que sigui un mapa local, una part més petita i concreta dins l'esfera.
• Àrea: Extensió o superfície relativa dels territoris representats en el mapa.
• Distància: La línia que es pot traçar entre dos punts i que equival a la mateixa longitud.
• Escala: Proporció entre les distàncies mesurades al mapa i les dels territoris representats.

Actualment, però, la majoria dels mapes es fan a partir de projeccions modificades o combinacions d’altres per corregir aquestes distorsions i obtenir mapes més adequats per a cada situació.

L’equilibri just per a la funció específica

Un cop acceptat que totes les projeccions són inexactes, cartògrafs i matemàtics fa centenars d’anys que intenten trobar les fórmules que compleixin millor l’objectiu per al qual es vol crear cada mapa buscant l’equilibri entre les distorsions. La indicatriu de Tissot (cercles vermells) ens ajuda a visualitzar la distorsió de cada mapa: observem com la projecció de Mercator (esquerra) conserva molt bé les formes però varia molt l’àrea en latituds altes; en canvi, la projecció de Gall-Peters (dreta) conserva molt fidelment l’extensió dels països però els deforma completament.

Una projecció és equivalent si manté les proporcions entre les àrees, equidistant si manté les distàncies respecte a un o més punts determinats i conforme si manté les formes (els angles) localment. Un altre tipus són les afilàctiques: sense mantenir pròpiament cap de les propietats, aconsegueixen una certa solució de compromís entre elles.

Connectats a la projecció de Mercator

Una de les projeccions universalment més famoses és la de Mercator, creada pel cartògraf i geògraf flamenc Gerardus Mercator el 1569. Va consolidar-se com la projecció estàndard per a propòsits navals gràcies a la seva capacitat de representar línies en una direcció real constant (és a dir, com mantenint la direcció en una brúixola), de vital importància en una època en què a la navegació només es guiaven per la direcció. Malgrat les distorsions d’àrea, està considerada generalment una projecció conforme (que manté les formes), sobretot si ens centrem en zones petites del mapa.

Una projecció tan consolidada s’ha adaptat als nous temps, dins d’uns límits, fins al punt que l’OTAN la va utilitzar com a base per establir un sistema internacional de coordenades. Avui la projecció Mercator s’usa en quasi totes les aplicacions de mapes que tots consultem sovint. El que sabem del cert, però, és que mai serà tan exacta com una esfera.

Altres projeccions significatives de la Terra